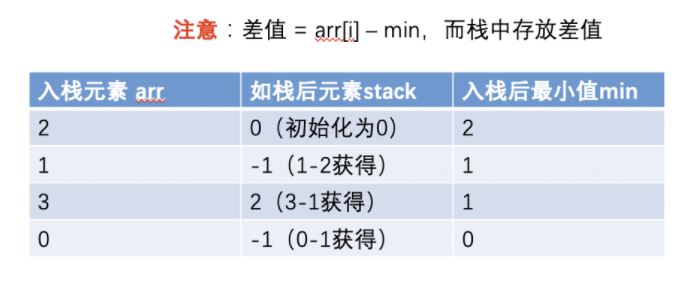
什么是二叉树（上）

a数据结构入门 4月前 0 9

欢迎大家来到这期知识大讲堂，今天我向大家介绍什么是二叉树，在此之前，大家需了解什么是树?
树是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。树是由结点和边组成的，不存在环的一种数据结构。通过下图，我们就可以更直观的认识树的结构。

看完了树的结构，我再给个图展示非树的结构:

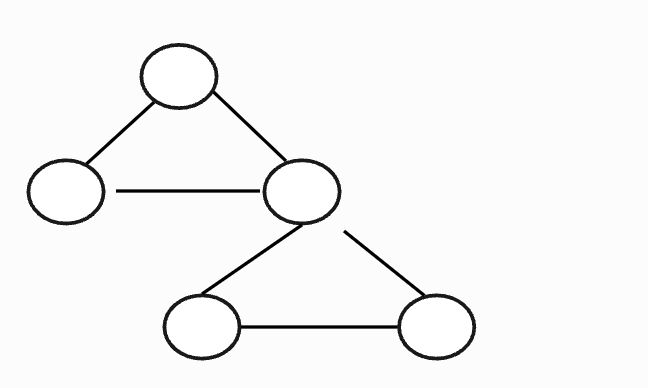
通过以上图示我们可以初步了解树的基本特点:
1.树中的每个元素都被称为节点。节点可以包含数据和指向其他节点的链接.
2.树中各个节点相连，但不会有环。
3.每棵树都只有一个根节点，还有若干个父节点,叶子节点。
到这里想必大家对树有了一个基本的了解。除此之外，关于树还有几个概念大家要熟知于心,比如，高度，深度，层，宽度等。画张图对照着讲解:

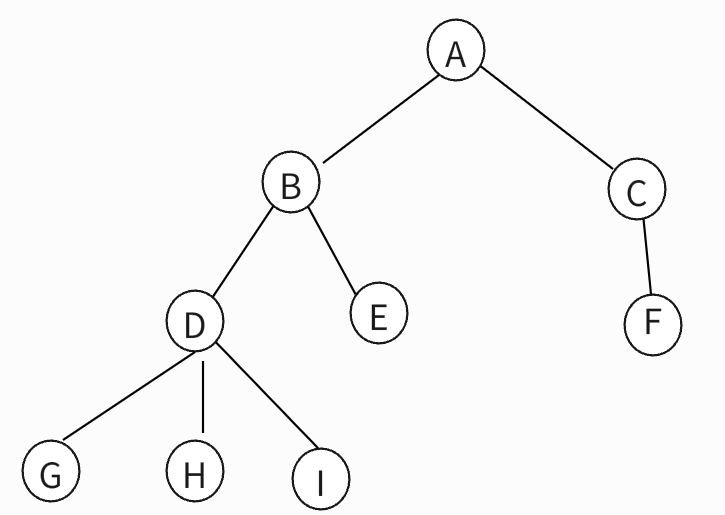
层:从根节点开始算起，根节点算第一层。如节点A处于第一层，B,C节点处于第二层，以此类推。
高度:指从该节点最底层的叶子节点出发，自底向上逐层累加至该结点时的高度。树的高度是树中高度最大的结点的高度。
如G节点高度为0,D节点高度为1。
深度:指从根节点自顶向下逐层累加至该结点时的深度。树的深度是树中深度最大的结点的深度。比如A节点深度为0,C节点深度为1.
宽度:把结点的子树的棵树称为结点的宽度，树的宽度是树中宽度最大的结点的宽度。如D节点的宽度为3;
树的结构多种多样,但用的最多的还是二叉树.接下来就向大家介绍什么是二叉树?
二叉树，顾名思义,每个节点最多有两个子节点，通常被称为左子节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。我画了几张图大家可以看下:

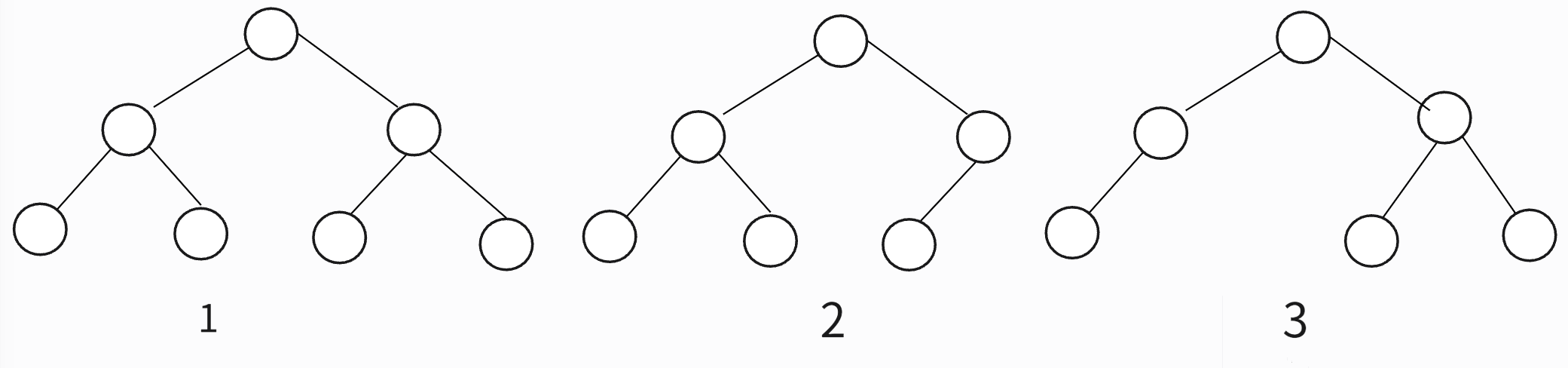
观察细致的小伙伴会发现这个图里面有两个比较特殊的二叉树，图1的叶子节点全部在最底层,除了叶子节点之外，每个节点都有左右两个子节点。这种二叉树叫做满二叉树。图2的叶子节点全在最底层，除了叶子节点之外,不是每个节点都有左右两个子节点,而且叶子节点都靠左紧密排列且其他层的叶子节点个数达到最大，这种二叉树叫做完全二叉树。对于满二叉树来说想必大家很好理解，但对于完全二叉树来说，初学者可能有一点点困难。让我来给大家解开这个谜底。先带大家直观的感受一下非完全二叉树，如上面图3所示，许多同学可能会疑惑这也没区别啊，细微一看还是有点区别。就是最底层的叶子节点没有紧密排列，缺失了满足完全二叉树的条件。但从表面图示来看并不能完全的解开大家疑惑，还得从实际的应用层面来深入。我们得首先知道如何来存储一颗二叉树?一般有两种方法，一种是基于引用的二叉链式存储法，另一种是基于数组的顺序存储法。今天重点介绍基于数组的顺序存储法,如下图所示:

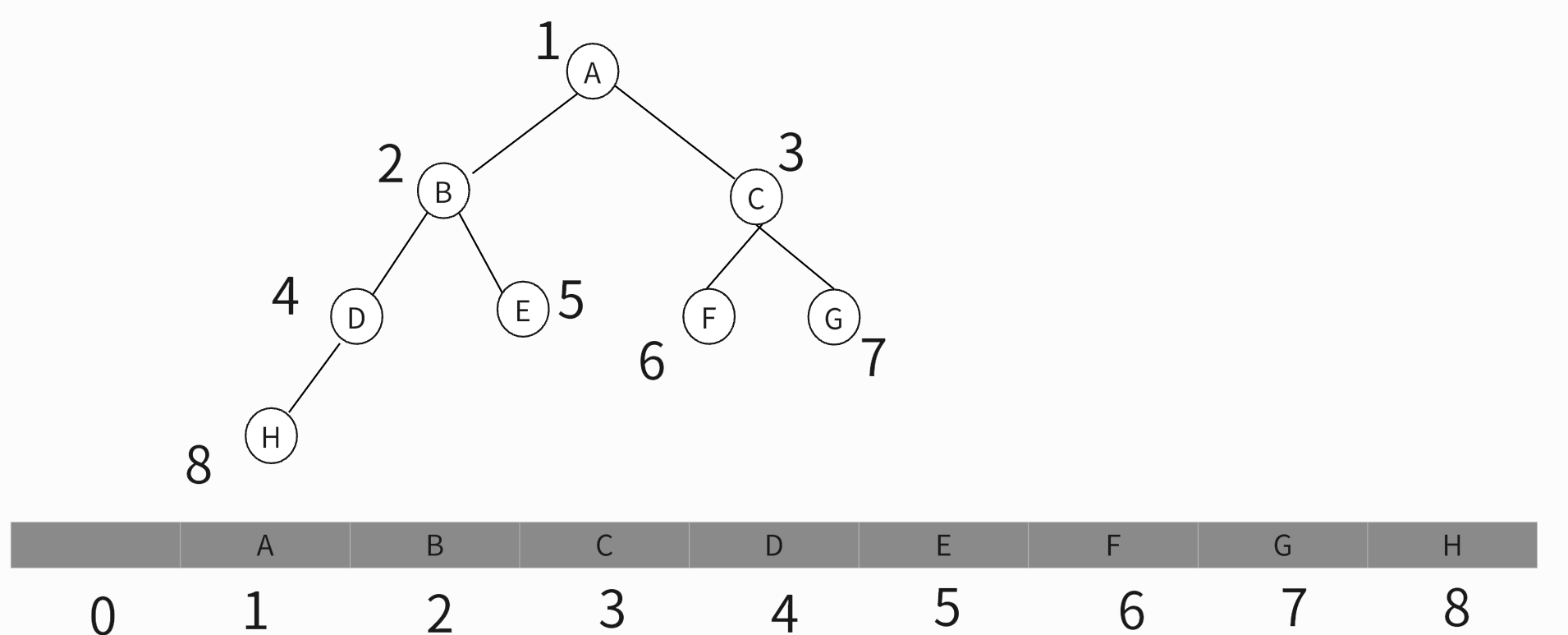
首先将根节点的值存储在下标为i=1的位置，然后将它的左子节点存储在下标为2i的位置为2,右子节点存储在2i+1的位置为3，以此类推,B节点的左子节点存储在2*2=4的位置。我来做个小小的总结,如果节点X存储在数组中下标为i的位置，下标为2 * i 的位置存储的就是左子节点，下标为2 * i + 1的位置存储的就是右子节点。反过来，下标为i/2的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为1的位置），这样就可以通过下标计算，把整棵树都串起来。
看完了完全二叉树的顺序存储，我们再来看非完全二叉树的基于数组的顺序存储，如下图所示:

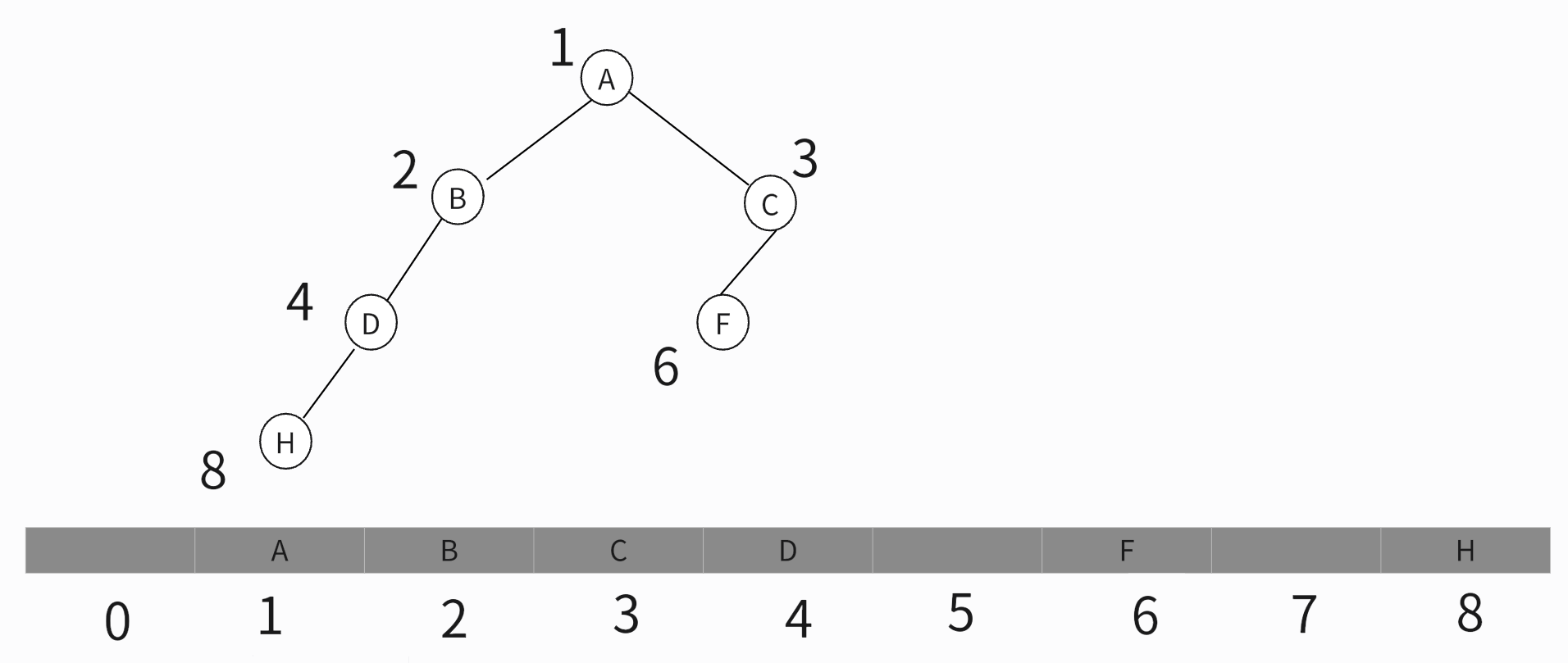
可以看出非完全二叉树在存储节点的值时会浪费一定的内存空间，导致计算机资源的浪费。如图中数组下标为5和7的内存空间浪费了。所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因。