什么是数组？

在入门编程那会，相信大家都学过数组，不过对于很多初学者，很多人可能仅仅只是会使用数组而已，并不理解数组的底层原理，如果你对数组的内存模型比较懂的话，那么你学起链表等也会变的很容易，所以这篇文章，我带大家重新来学习下数组。

数组的底层实现原理

什么是数组？按照官方的定义，数组可以被定义为是一组被保存在连续存储空间中，并且具有相同类型的数据元素集合。而数组中的每一个元素都可以通过自身的索引（Index）来进行访问，这也是数组可以被高效访问的原因。

下面就以 Java 语言中的一个例子来说明一下数组的内存模型，当定义了一个拥有 5 个元素的 int 数组后，来看看内存长什么样子。

int[] data = new int[5] ;// 定义一个大小为 5 的数组

通过上面这段声明，计算机会在内存中分配一段连续的内存空间给这个 data 数组。现在假设在一个 32 位的机器上运行这段程序，Java 的 int 类型数据占据了 4 个字节的空间，同时也假设计算机分配的地址是从 0x80000000 开始的，整个 data 数组在计算机内存中分配的模型如下图所示。

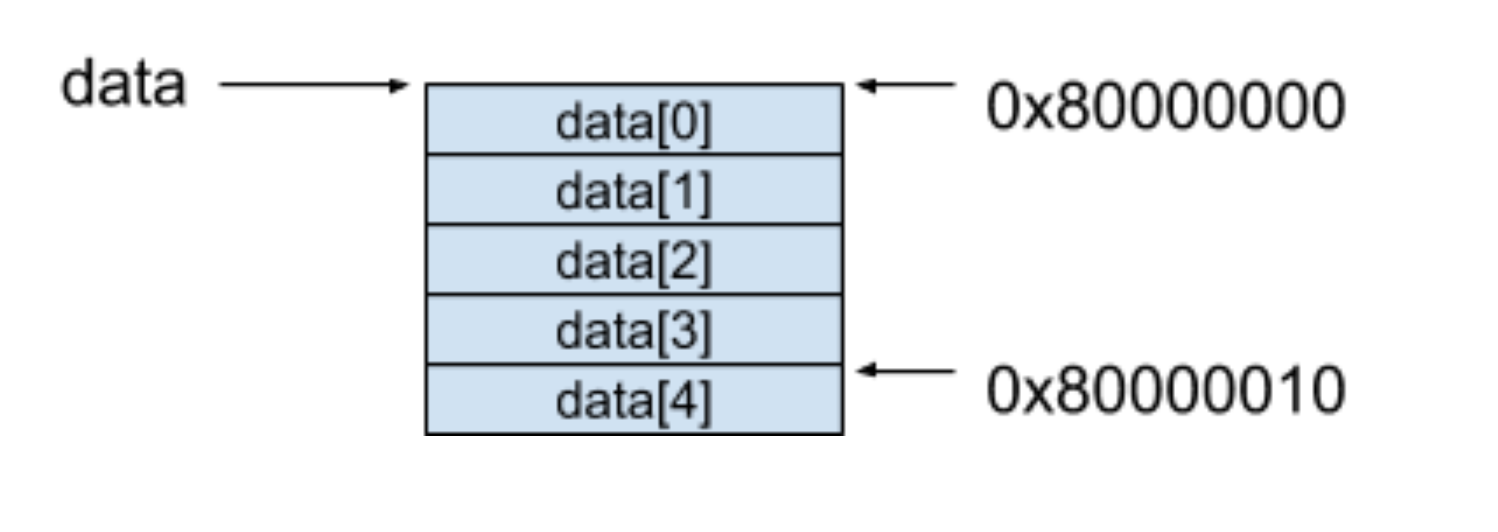
这种分配连续空间的内存模型同时也揭示了数组在数据结构中的另外一个特性，即随机访问（Random Access）。随机访问这个概念在计算机科学中被定义为：可以用同等的时间访问到一组数据中的任意一个元素。这个特性除了和连续的内存空间模型有关以外，其实也和数组如何通过索引访问到特定的元素有关。

刚接触计算机时的你，不知是否会有这样的一个疑惑：为什么在访问数组中的第一个元素时，程序一般都是表达成以下这样的：

data[0]

也就是说，数组的第一个元素是通过索引“0”来进行访问的，第二个元素是通过索引“1”来进行访问的，……，这种从 0 开始进行索引的编码方式被称为是“Zero-based Indexing”。当然了，在计算机世界中也存在着其他的索引编码方式，像 Visual Basic 中的某些函数索引是采用 1-based Indexing 的，也就是说第一个元素是通过“1”来获取的，但这并不在我们这一讲的讨论范围内，大家可自行查询资料了解详情。

我们回到数组中第一个元素通过索引“0”来进行访问的问题上来，之所以采取这样的索引方式，原因在于，获取数组元素的方式是按照以下的公式进行获取的：

base_address + index（索引）× data_size（数据类型大小）

索引在这里可以看作是一个偏移量（Offset），还是以上面的例子来进行说明。

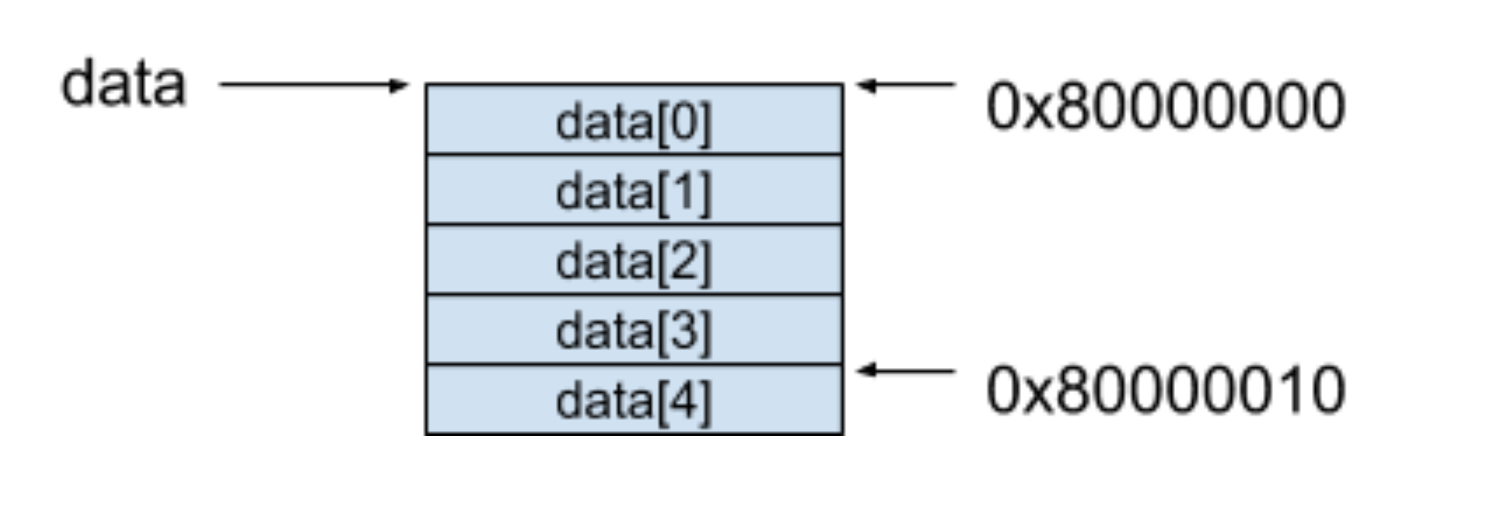
data 这个数组被分配到的起始地址是 0x80000000，是因为 int 类型数据占据了 4 个字节的空间，如果我们要访问第 5 个元素 data[4] 的时候，按照上面的公式，只需要取得 0x80000000 + 4 × 4 = 0x80000010 这个地址的内容就可以了。随机访问的背后原理其实也就是利用了这个公式达到了同等的时间访问到一组数据中的任意元素。

数组的查找操作

刚才说了数组支持随机访问，通过索引访问任何一个数组的时间都是相同的，例如你要访问内存中的第三个元素，则直接 date[2] 就可以访问到了，数组中的任意元素，都可以很方便着通过索引值 index 来快速访问到，且时间复杂度为 O(1)，这也是数组的一个巨大优势。

不过，另外一种基于数值的查找方法，数组就没有什么优势了。例如，查找数值为 7 的元素是否出现过，以及如果出现过，索引值是多少。这种基于数值属性的查找操作，由于我们不知道索引值 index 是多少，导致我们需要整体遍历一遍数组的，这种查找操作就很慢了，需要 O(n) 的时间复杂度。

数组的新增操作

数组新增数据有两个情况：

第一种情况，在数组的最后增加一个新的元素。此时新增一条数据后，对原数据没有产生任何影响。可以直接通过新增操作，赋值或者插入一条新的数据即可，时间复杂度是 O(1)。

第二种情况，如果是在数组中间的某个位置新增数据，那么情况就完全不一样了。这是因为，新增了数据之后，会对插入元素位置后面的元素产生影响，为了给这个插入的元素让出一个空位，后面的元素需要一次次向后挪动 1 个位置。

例如，对于某一个长度为 5 的数组，

我们在第 2 个元素之后插入一个元素 8，那么修改后的数组中就包含了 6 个元素，其中第 1、第 2 个元素不发生变化，后面的元素需要往后移动。而这个移动操作，与数组的数据量线性相关，因此时间复杂度是 O(n)。

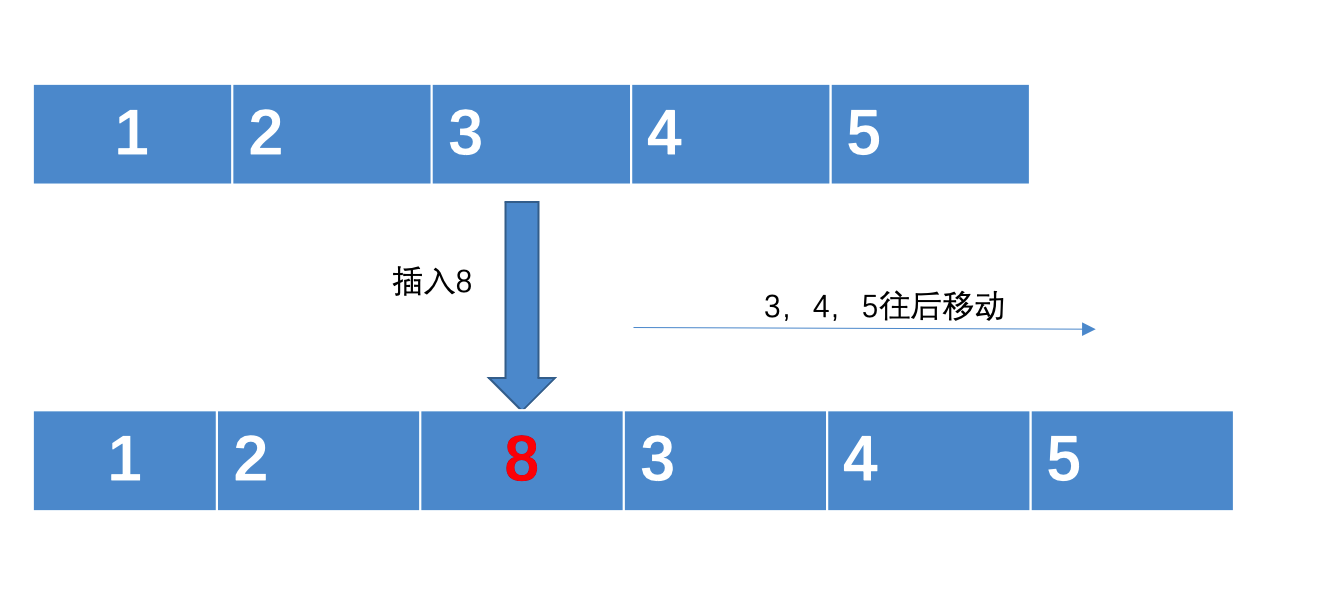
数组的新增操作

删除和新增差不多的，也是分两种情况。

第一种情况，在这个数组的最后，删除一个数据元素。由于此时删除一条数据后，对原数据没有产生任何影响。我们可以直接删除该数据即可，时间复杂度是 O(1)。

第二种情况，在这个数组的中间某个位置，删除一条数据。同样的，这两种情况的区别在于，删除数据之后，其他数据的位置是否发生改变。

这里就不举例子了。

数组案例

问题描述：假设数组存储了 5 个评委对 1 个运动员的打分，且每个评委的打分都不相等。现在需要你：

1、用数组按照连续顺序保存，去掉一个最高分和一个最低分后的 3 个打分样本；

2、计算这 3 个样本的平均分并打印。

3、要求是，不允许再开辟 O(n) 空间复杂度的复杂数据结构。

解答：我们先分析一下题目：第一个问题，要输出删除最高分和最低分后的样本，而且要求是不允许再开辟复杂空间。因此，我们只能在原数组中找到最大值和最小值并删除。第二个问题，基于删除后得到的数组，计算平均值。所以解法如下：

1、数组一次遍历，过程中记录下最小值和最大值的索引。对应下面代码的第 7 行到第 16 行。时间复杂度是 O(n)。

2、执行两次基于索引值的删除操作。除非极端情况，否则时间复杂度仍然是 O(n)。对应于下面代码的第 18 行到第 30 行。

3、计算删除数据后的数组元素的平均值。对应于下面代码的第 32 行到第 37 行。时间复杂度是 O(n)。

因此，O(n) + O(n) + O(n) 的结果仍然是 O(n)。代码如下

public void getScore() {
    int a[] = { 2, 1, 4, 5, 3 };
    max_inx = -1;
    max_val = -1;
    min_inx= -1;
    min_val = 99;
    for (int i = 0; i < a.length; i++) {
        if (a[i] > max_val) {
        max_val = a[i];
        max_inx = i;
    }
    if (a[i] < min_val) {
        min_val = a[i];
        min_inx = i;
    }
    }

    inx1 = max_inx;
    inx2 = min_inx;
    if (max_inx < min_inx){
        inx1 = min_inx;
        inx2 = max_inx;
    }
    for (int i = inx1; i < a.length-1; i++) {
        a[i] = a[i+1];
    }
    for (int i = inx2; i < a.length-1; i++) {
        a[i] = a[i+1];
    }
    sumscore = 0;
    for (int i = 0; i < a.length-2; i++) {
        sumscore += a[i];
    }
    avg = sumscore/3.0;
    System.out.println(avg);
}

总结

之所以花这么多篇幅来讲数组，主要也是为了和后面的链表进行对比。

shuaidi永久会员

收藏 海报挣佣金 推广链接