剑指 Offer 34. 二叉树中和为某一值的路径
本问题对应的 leetcode 原文链接:剑指 Offer 34. 二叉树中和为某一值的路径
问题描述
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例1 :
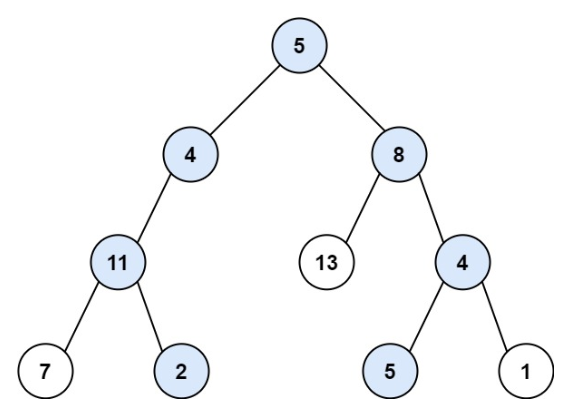
示例2 :
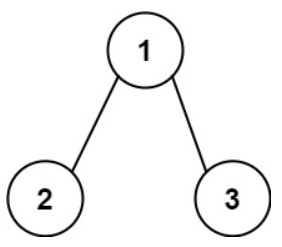
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
- 提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
- 树中节点总数在范围
解题思路
视频讲解直达: 本题视频讲解
代码实现
时间复杂度:O(n)
空间复杂度:O(n)

