漫画:什么是归并排序算法?
归并排序是建立在归并操作的一种高效的排序方法,该方法采用了分治的思想,比较适用于处理较大规模的数据,但比较耗内存,今天我们聊聊归并排序
一、排序思想
一天,小一尘和慧能坐在石头上,眺望着远方





分而治之: 分开来去治理



归并即合并之意
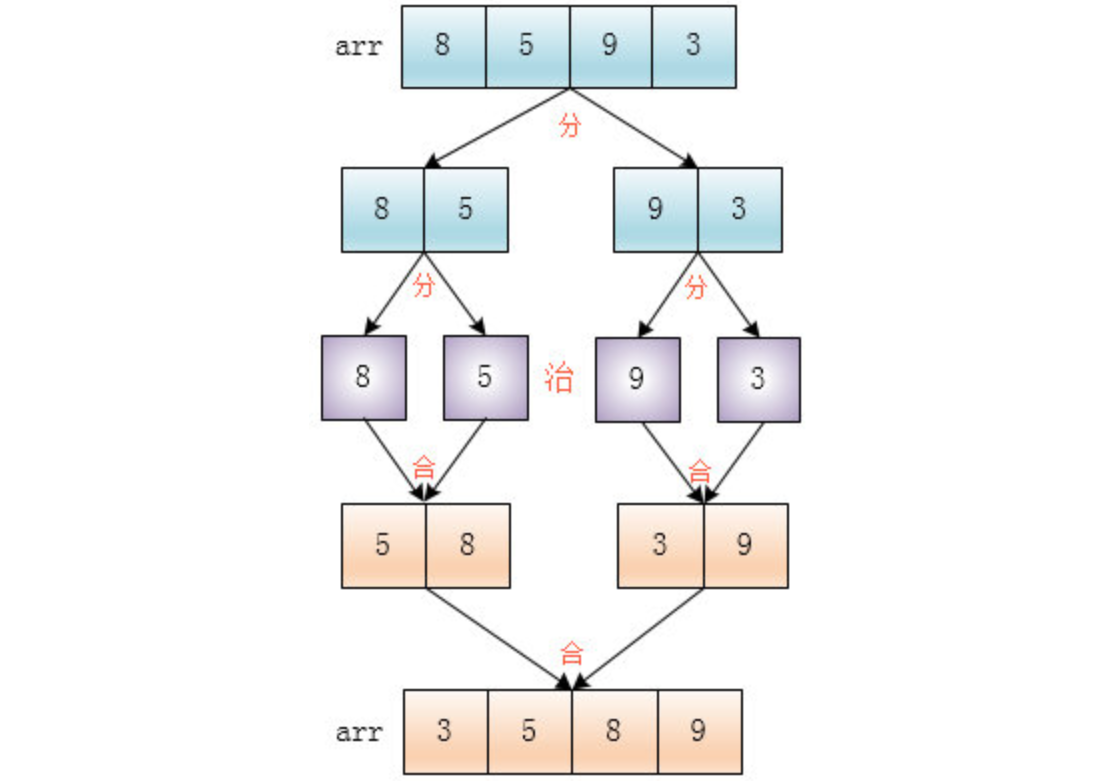
慧能随手画了一张图解释了一下
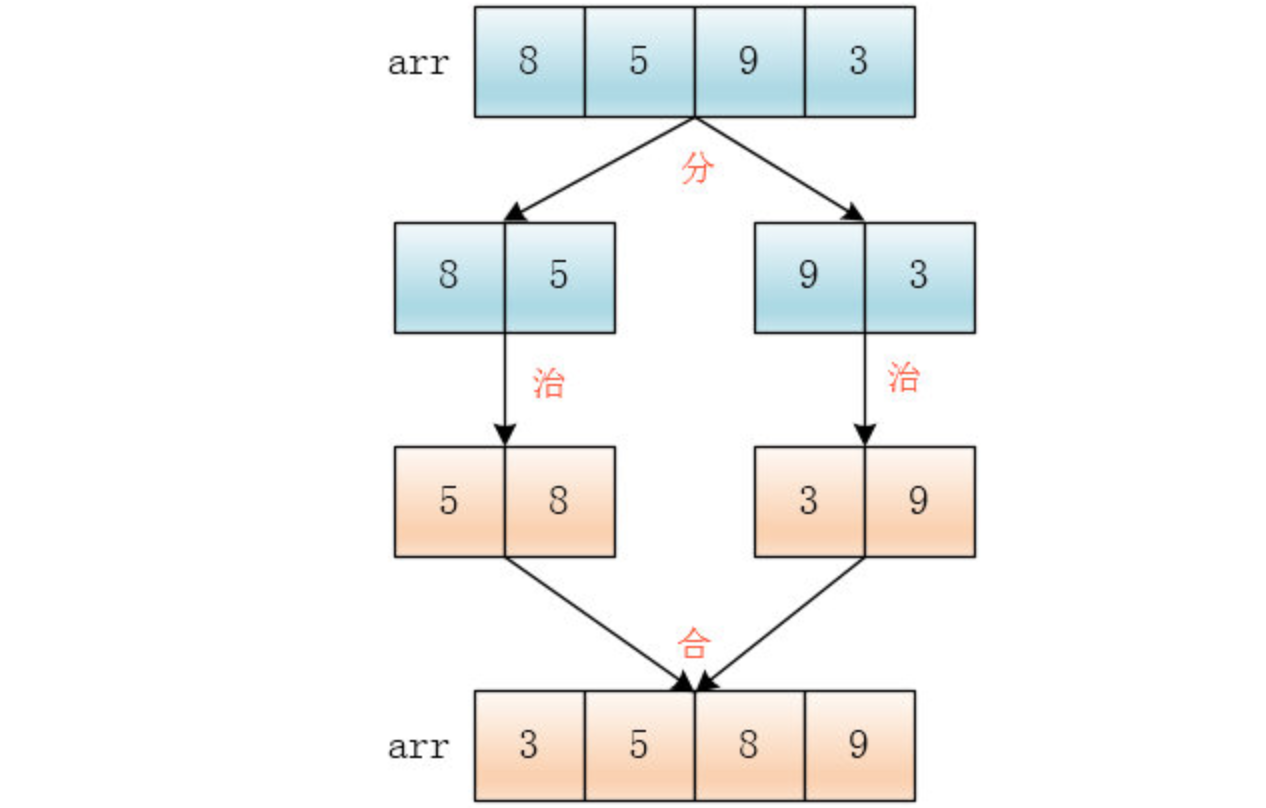
治:治理,这里就是将数组排序


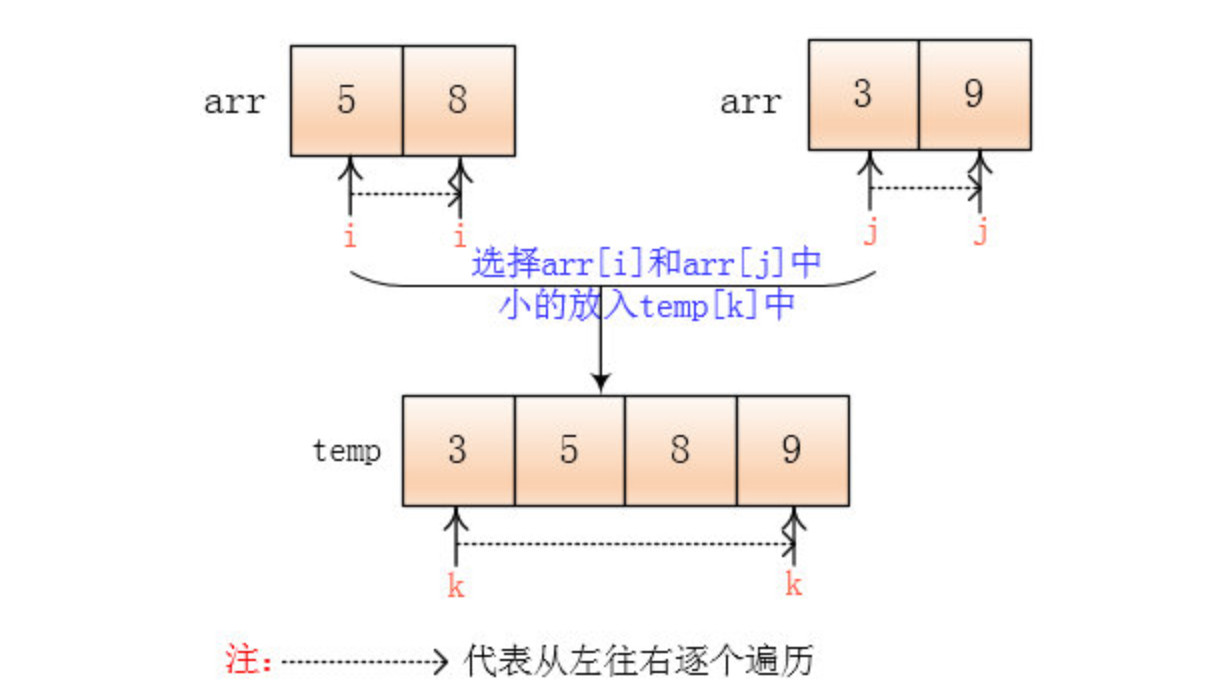
对于合并,其实非常简单,我只要不断地取出两个有序数组中比较小的那一个放在一个辅助数组中(通过比较),直到把两个有序数组中的元素取完

二、代码


一尘已经了解了师傅的固定套路了
既然是不断地分,那用递归就非常简单了,什么时候终止递归呢?递归到只有一个元素的时候。一尘随手写下了如下代码

这里需要说明的是,center = (left + right) / 2 最好改成 center = left + (right – left) / 2,因为 left + right 有可能溢出。
很快,一尘写下了 merge 函数的代码


三、时间复杂度

一尘想到:这个有点烧脑啊,元素个数为 n,运行时间是多少啊?递归,递归,再递归…

师傅一下看出了一尘的心思


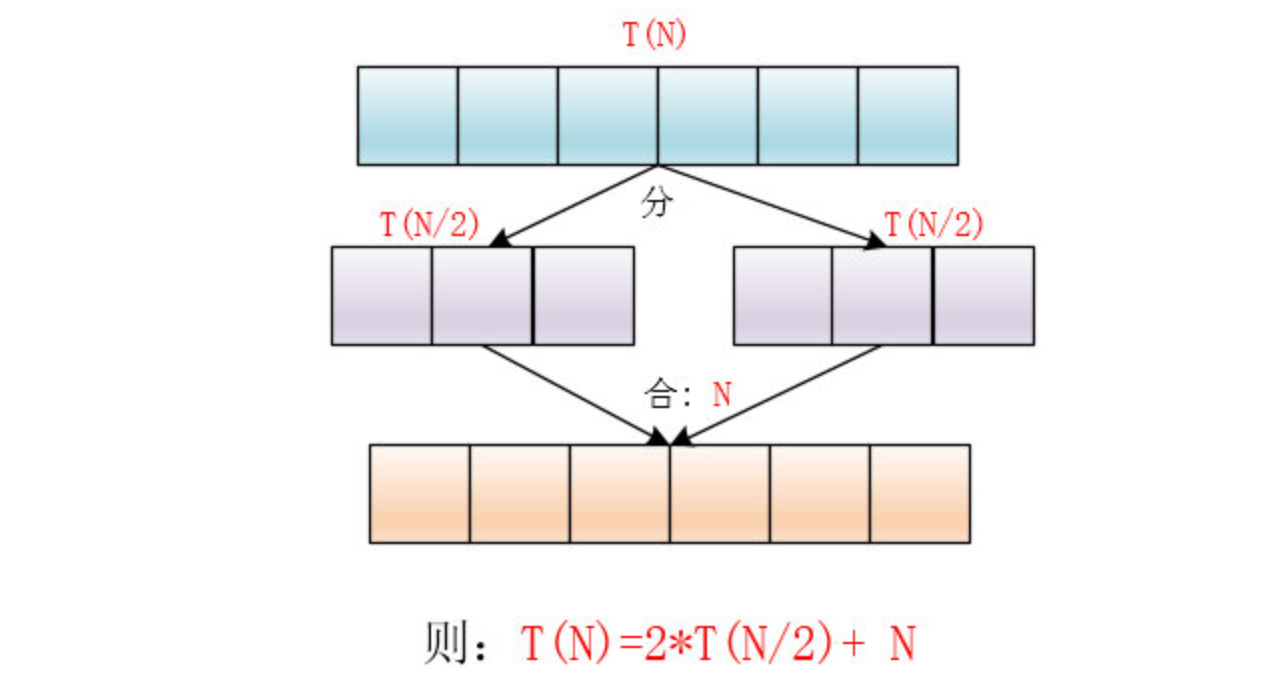
假设处理的数据规模大小为 N
运行时间设为:T(N)
① 当把 N 分为两半时,那么处理大小为 N/2 子数组花费时间为:T(N/2)
② 合并花费时间与数据规模成正比:N
所以处理规模大小为N的数据所需要花费两个大小为 N/2 的子数组加上合并花费的时间
即:T(N) = 2T(N/2) + N
对于 N = 1,T(1) = 1


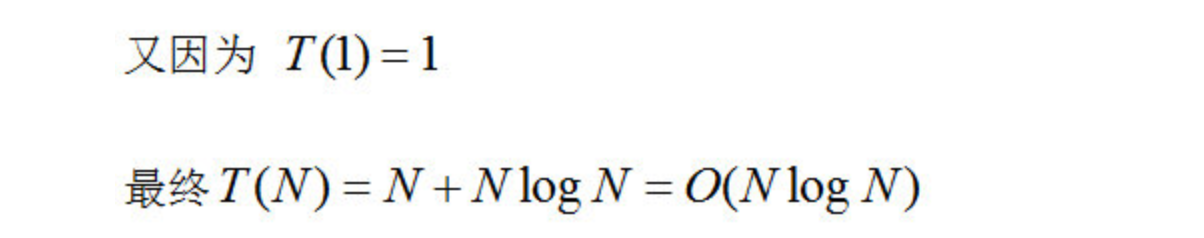


四、稳定性



此时太阳已经下山,一尘和师傅走在回家的路上,在路上,一尘脑子又想了一下归并排序的全过程



评论(1)
所以最后稳定性也没说