什么是二叉树(下)
上一篇文章中介绍了树,二叉树,满二叉树,完全二叉树,非完全二叉树等知识点,有句古话说的好,光说不练假把式,我们只学了理论,但是如何用代码将二叉树实现呢?下面让我来教大家一一入门。在此之前我们得先了解什么是二叉树的遍历?它有几种遍历方法?二叉树的遍历是指访问树中所有节点的过程,按照一定的顺序访问每个节点。最常见的二叉树遍历方法有三种:前序遍历、中序遍历和后序遍历。每种遍历方式访问节点的顺序不同:
- 前序遍历(Pre-order Traversal):
- 访问根节点。
- 遍历左子树。
- 遍历右子树。
前序遍历的顺序是:根节点 -> 左子树 -> 右子树。
- 中序遍历(In-order Traversal):
- 遍历左子树。
- 访问根节点。
- 遍历右子树。
中序遍历的顺序是:左子树 -> 根节点 -> 右子树。
- 后序遍历(Post-order Traversal):
- 遍历左子树。
- 遍历右子树。
- 访问根节点。
后序遍历的顺序是:左子树 -> 右子树 -> 根节点。
介绍完了遍历方法,那我们怎么实现呢?我们先创建好一颗二叉树如图所示,然后用前序遍历,中序遍历,后序遍历来输出二叉树的遍历节点值;
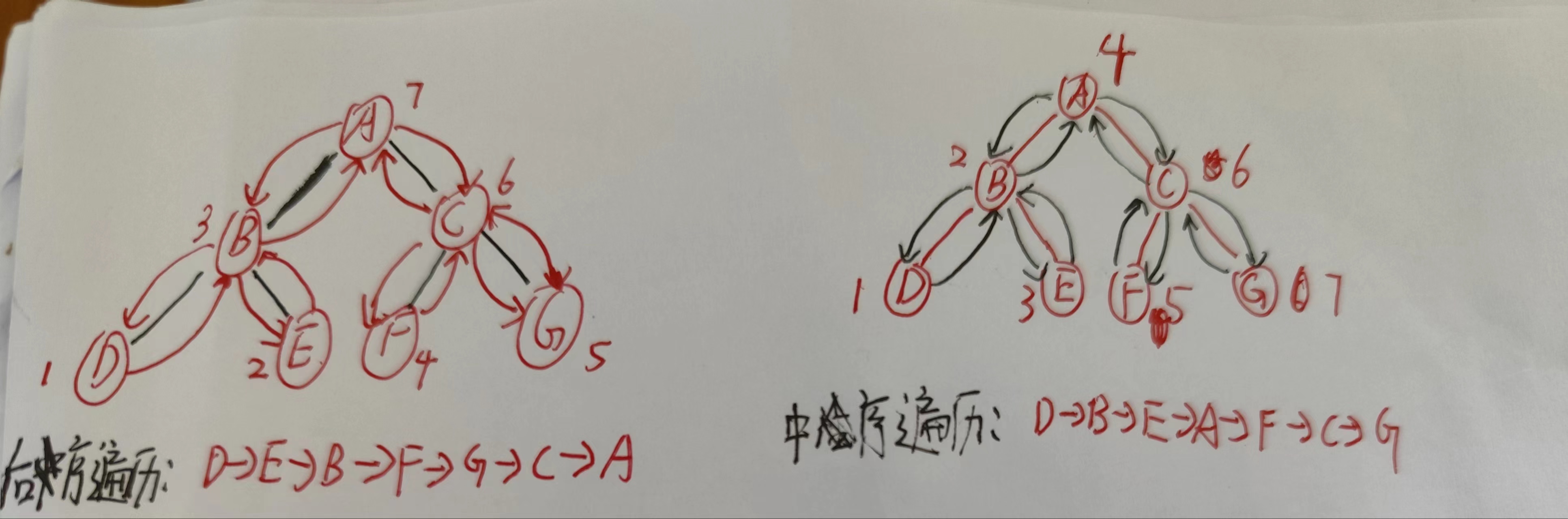

那代码怎么写呢?二叉树的前、中、后序遍历就是一个递归的过程。递归一般有三个步骤,第一先明确你的函数要做什么,然后找到这个函数的终止条件,就是找递归到终点的条件 ,最后写递推关系式. 比如,前序遍历,其实就是先打印根节点,然后再递归地打印左子树,最后递归地打印右子树。写递归代码的关键,就是看能不能写出递推公式,而写递推公式的关键就是,如果要解决问题A,就假设子问题B、C已经解决,然后再来看如何利用B、C来解决A。所以,我们可以把前、中、后序遍历的递推公式先写出来,再来完善。完整的前,中,后序遍历代码如下:
// 前序遍历打印二叉树的元素
public void preorderTraversal(TreeNode root) {
if (root == null) {//终止条件
return;
}
System.out.print(root.val + " ");
preorderTraversal(root.left);//递推公式
preorderTraversal(root.right);//递推公式
}
// 中序遍历
public void inorderTraversal(TreeNode root) {
if (root == null) {
return;
}
inorderTraversal(root.left);
System.out.print(root.val + " ");//递推公式
inorderTraversal(root.right);//递推公式
}
// 后序遍历
public void postorderTraversal(TreeNode root) {
if (root == null) {//终止条件
return;
}
postorderTraversal(root.left);//递推公式
postorderTraversal(root.right);//递推公式
System.out.print(root.val + " ");
}
介绍完了二叉树的三种遍历方法,聪明的小伙伴可能会有疑问,那光有遍历的方法可不行,还得有
创建初始化二叉树的方法,一般也可以根据前,中,后三种遍历方式创建,这样才可以动态的对数据集进行输入输出操作。完整的代码如图所示:(该图中采用前序遍历的列表构建二叉树,中序,后序类似,剩下的交给你自己去实现,聪明的你一定可以的)
// 定义二叉树节点类
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class BinaryTree {
// 根据前序遍历的列表构建二叉树,对传入的数组值做一个判断
public TreeNode buildTree(int[] preorder) {
if (preorder == null || preorder.length == 0) {
return null;
}
return buildTree(preorder, 0, preorder.length - 1);
}
private TreeNode buildTree(int[] preorder, int start, int end) {
if (start > end) {//终止条件,如果没有区间元素构建了,则返回空.
return null;
}
//构建该节点的根节点
TreeNode root = new TreeNode(preorder[start]);
//构建二叉树的左右子树与根节点的大小关系
int i = start + 1;
while (i <= end && preorder[i] > preorder[start]) {
i++;
}
root.left = buildTree(preorder, start + 1, i - 1);//构建左子树
root.right = buildTree(preorder, i, end);//构建右子树
return root;
}
// 前序遍历打印二叉树的元素
public void preorderTraversal(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
preorderTraversal(root.left);
preorderTraversal(root.right);
}
// 中序遍历
public void inorderTraversal(TreeNode root) {
if (root == null) {
return;
}
inorderTraversal(root.left);
System.out.print(root.val + " ");
inorderTraversal(root.right);
}
// 后序遍历
public void postorderTraversal(TreeNode root) {
if (root == null) {
return;
}
postorderTraversal(root.left);
postorderTraversal(root.right);
System.out.print(root.val + " ");
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
//用前序遍历的方式构建二叉树
int[] preorderTraversalArray = {5, 3, 2, 4, 1};
TreeNode root = tree.buildTree(preorderTraversalArray);
//前序遍历
System.out.println("前序遍历结果:");
tree.preorderTraversal(root);
//中序遍历
System.out.println("中序遍历结果:");
tree.inorderTraversal(root);
//后序遍历
System.out.println("后序遍历结果:");
tree.postorderTraversal(root);
}
}
应用场景:
学完了二叉树的创建与实现,我们再来了解一下它的应用场景。二叉树是一种比较重要的数据结构,在Mysql关系型数据库中,B树和B+树是数据库索引中常用的数据结构,它们允许快速的数据检索。还有许多文件系统用B树,B+树来组织文件和目录等等。
今日小结:
今天我给大家介绍了二叉树的三种最常见的遍历方式,有前序遍历,中序遍历,后序遍历等,除了介绍理论知识外,我还教大家如何实现前中后遍历的代码,但这又会衍生出一个问题,该如何构建初始的二叉树呢?构建二叉树也有三种对应的方法,有通过前序遍历的列表构建二叉树,中序,后序等。知识的学习是无止境的,关键在于大家的坚持。
