什么是trie树?
Trie 树大家了解一下原理和应用即可,有时候面试的时候会问到,下面我用面试的情景跟大家讲解 trie 树。
面试官:玩过王者荣耀吧?了解过敏感词过滤吗?,例如在游戏里,如果我们发送“你在干嘛?麻痹演员啊你?”,由于“麻痹”是一个敏感词,所以当你把聊天发出来之后,我们会用“**”来代表“麻痹”这次词,所以发送出来的聊天会变成这样:“你在干嘛?**演员啊你?”。
小秋:听说过啊,在各大社区也经常看到,例如评论一个问题等,一些粗话经常被过滤掉了。
面试官:嗯,如果我给你一段文字,以及给你一些需要过滤的敏感词,你会怎么来实现这个敏感词过滤的算法呢?例如我给你一段字符串“abcdefghi”,以及三个敏感词”de”, “bca”, “bcf”。
小秋:(敏感词过来算法??不就是字符串匹配吗?)我可以通过字符串匹配算法,例如在字符串”abcdefghi”在查找是否存在字串“de”,如果找到了就把”de“用”**”代替。通过三次匹配之后,接变成这样了:“abc ** fghi”。
面试官:可以说说你采用哪种字符串匹配算法吗?
小秋:最简单的方法就是采用两个for循环保留求解了,不过每次匹配的都时间复杂度为O(n*m),我可以采用 KMP 字符串匹配算法,这样时间复杂度是 O(m+n)。
n 表示字符串的长度,m 表示每个敏感词的长度。
面试官:这是一个方法,对于敏感词过滤,你还有其他方法吗?
小秋:(其他方法?说实话,我也觉得不是采用这种 KMP 算法来匹配的了,可是,之前也没去了解过敏感词,这下要凉)对敏感词过来之前也没了解过,暂时没想到其他方法。
trie 树
面试官:了解过 trie 树吗?
小秋:(嘿嘿,数据结构这方法,我得争气点)了解过,我还用代码实现过。
面试官:可以说说它的特点吗?
小秋:trie 树也称为字典树、单词查找树,最大的特点就是共享字符串的公共前缀来达到节省空间的目的了。例如,字符串 “abc”和”abd”构成的 trie 树如下:
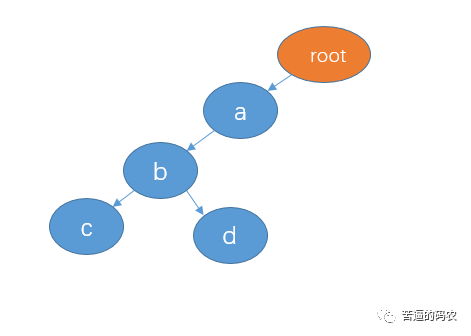
trie 树的根节点不存任何数据,每整个个分支代表一个完整的字符串。像 abc 和 abd 有公共前缀 ab,所以我们可以共享节点 ab。如果再插入 abf,则变成这样:
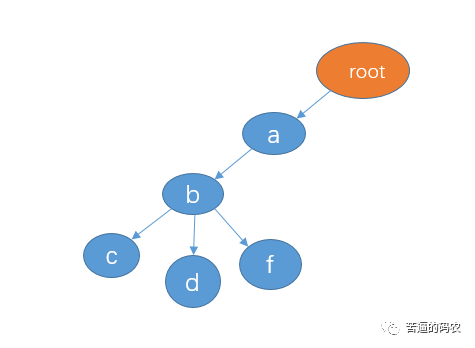
如果我再插入 bc,则是这样(bc 和其他三个字符串没有公共前缀)
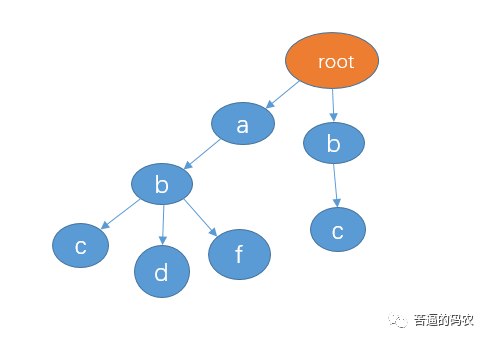
面试官:那如果再插入 “ab” 这个字符串呢?
小秋:差点说了,每个分支的内部可能也含有完整的字符串,所以我们可以对于那些是某个字符串结尾的节点做一个标记,例如 abc, abd,abf 都包含了字符串 ab,所以我们可以在节点 b 这里做一个标记。如下(我用红色作为标记):
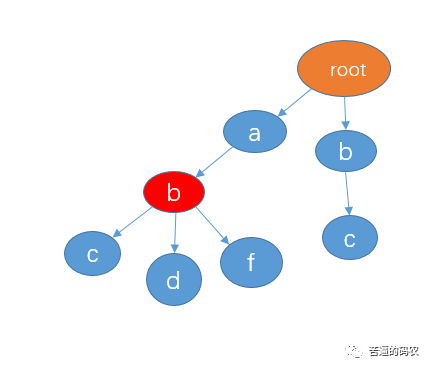
面试官:可以说说 trie 树有哪些应用吗?
小秋:trie 最大的特点就是利用了字符串的公共前缀,像我们有时候在百度、谷歌输入某个关键字的时候,它会给我们列举出很多相关的信息
这种就是通过 trie 树来实现的。
小秋:(嗯? trie 又称为单词查找树,好像可以用 trie 来实现刚才的敏感词匹配?面试官无缘无故提 trie 树难道别有用意?)
面试官:刚才的敏感词过滤,其实也可以采用 trie 来实现,你知道怎么实现吗?
trie 树来实现敏感词过滤
小秋:(果然,面试官真是个好人啊,直接提示了,要是还不知道怎么实现,那不真凉?)我想想……..我知道了,
我可以这样来实现:
先把你给我的三个敏感词:”de”, “bca”, “bcf” 建立一颗 trie 树,如下:
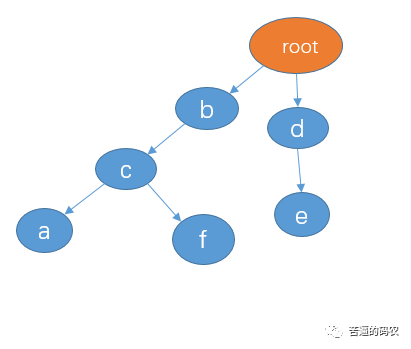
接着我们可以采用三个指针来遍历,我直接用上面你给你例子来演示吧。
1、首先指针 p1 指向 root,指针 p2 和 p3 指向字符串第一个字符
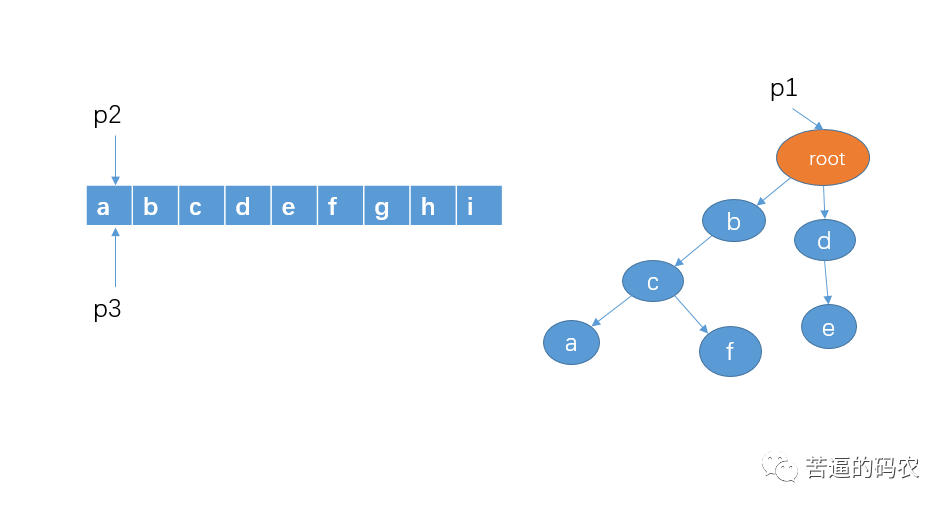
2、然后从字符串的 a 开始,检测有没有以 a 作为前缀的敏感词,直接判断 p1 的孩子节点中是否有 a 这个节点就可以了,显然这里没有。接着把指针 p2 和 p3 向右移动一格。
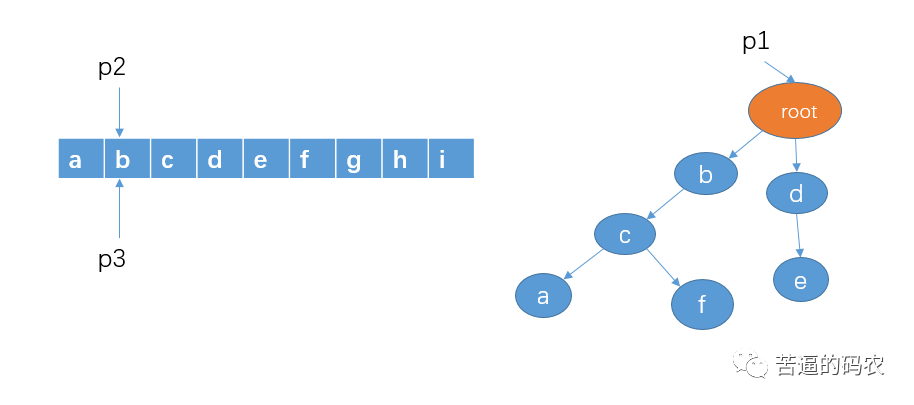
3、然后从字符串 b 开始查找,看看是否有以 b 作为前缀的字符串,p1 的孩子节点中有 b,这时,我们把 p1 指向节点 b,p2 向右移动一格,不过,p3不动。

4、判断 p1 的孩子节点中是否存在 p2 指向的字符c,显然有。我们把 p1 指向节点 c,p2 向右移动一格,p3不动。
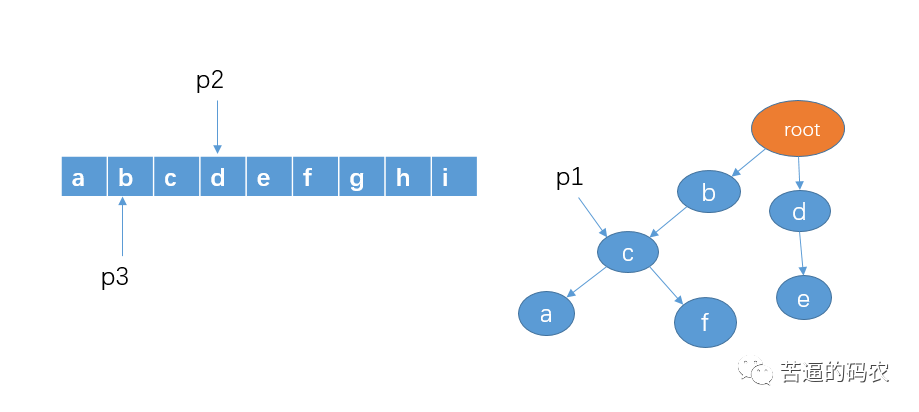
5、判断 p1 的孩子节点中是否存在 p2 指向的字符d,这里没有。这意味着,不存在以字符b作为前缀的敏感词。这时我们把p2和p3都移向字符c,p1 还是还原到最开始指向 root。
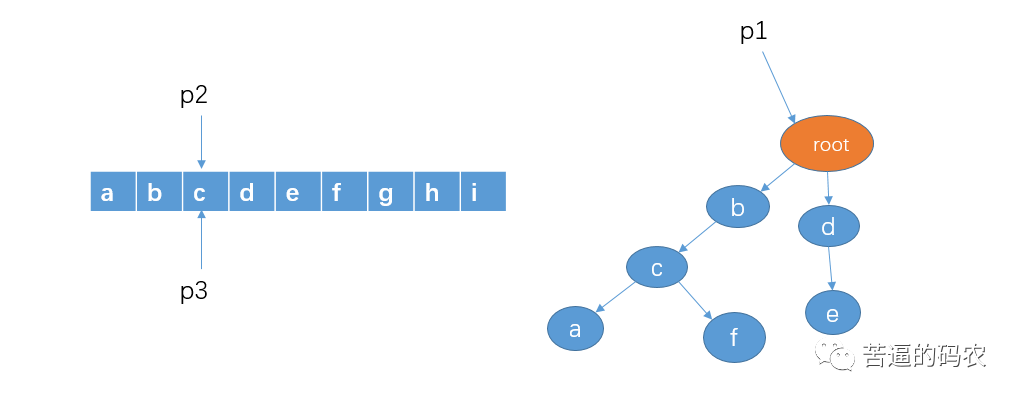
6、和前面的步骤一样,判断有没以 c 作为前缀的字符串,显然这里没有,所以把 p2 和 p3 移到字符 d。
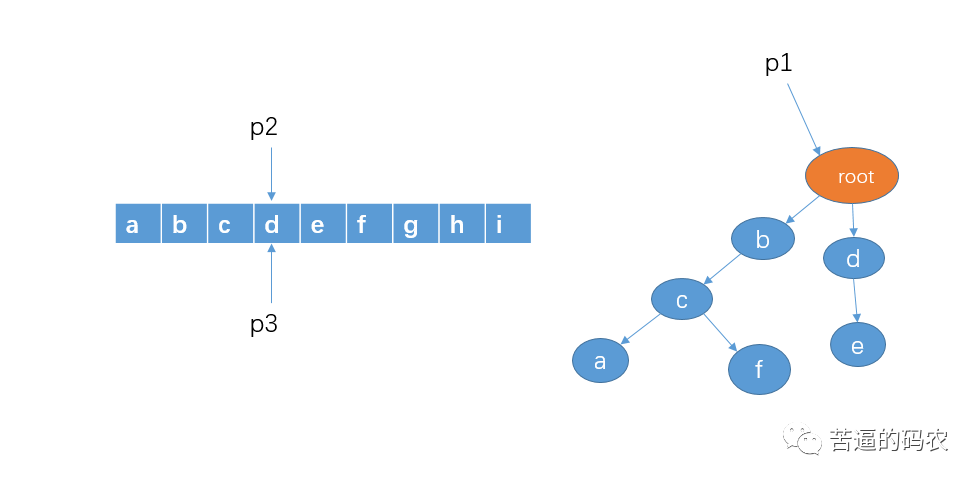
7、然后从字符串 d 开始查找,看看是否有以 d 作为前缀的字符串,p1 的孩子节点中有 d,这时,我们把 p1 指向节点 d,p2 向右移动一格,不过,p3和刚才一样不动。(看到这里,我猜你已经懂了)
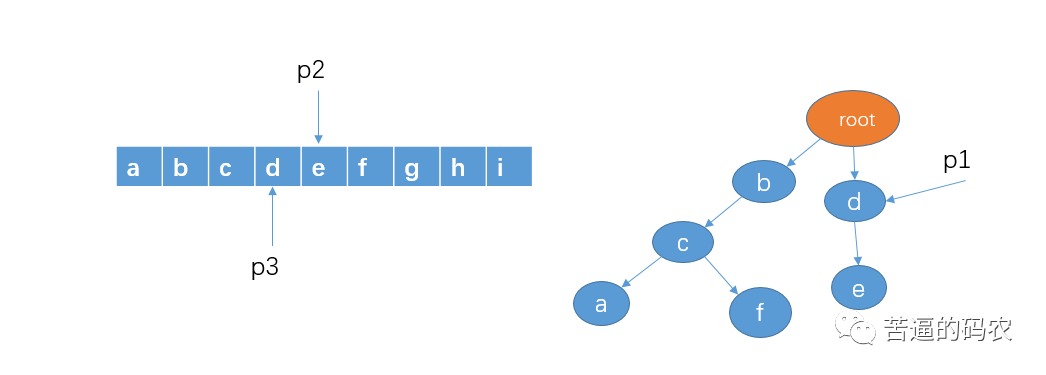
8、判断 p1 的孩子节点中是否存在 p2 指向的字符e,显然有。我们把 p1 指向节点 e,并且,这里e是最后一个节点了,查找结束,所以存在敏感词de,即 p3 和 p2 这个区间指向的就是敏感词了,把 p2 和 p3 指向的区间那些字符替换成 *。并且把 p2 和 p3 移向字符 f。如下:
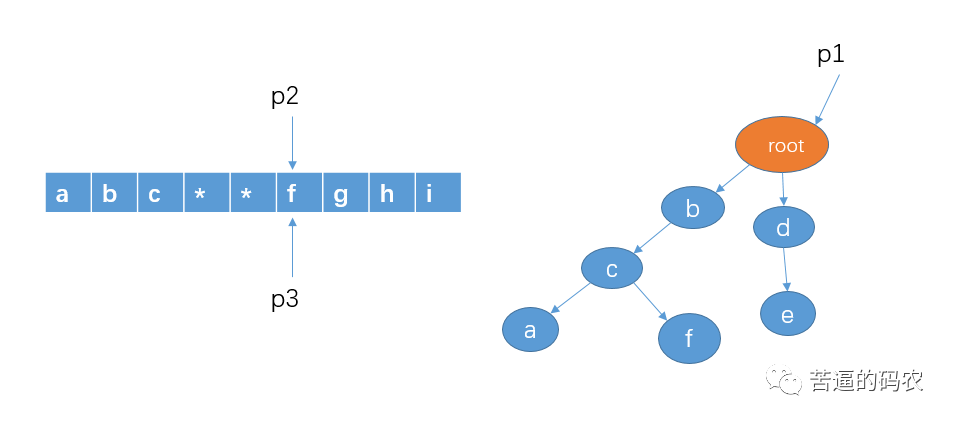
9、接着还是重复同样的步骤,知道 p3 指向最后一个字符。
复杂度分析
面试官:可以说说时间复杂度吗?
小秋:如果敏感词的长度为 m,则每个敏感词的查找时间复杂度是 O(m),字符串的长度为 n,我们需要遍历 n 遍,所以敏感词查找这个过程的时间复杂度是 O(n * m)。如果有 t 个敏感词的话,构建 trie 树的时间复杂度是 O(t * m)。
这里我说明一下,在实际的应用中,构建 trie 树的时间复杂度我觉得可以忽略,因为 trie 树我们可以在一开始就构建了,以后可以无数次重复利用的了。而刚才的 kmp 算法时间复杂度是 t *(m+n),不过kmp需要维护 next 数组比较费空间,而且在实际情况中,敏感词的数量 t 是比较大,而 n 反而比较小的吧。
10、如果让你来 构建 trie 树,你会用什么数据结构来实现?
小秋:我一般使用 Java,我会采用 HashMap 来实现,因为一个节点的字节点个数未知,采用 HashMap 可以动态拓展,而且可以在 O(1) 复杂度内判断某个子节点是否存在。
面试官:嗯,回去等通知吧。
总结
今天主要将了 trie 树以及 trie 树的一些应用,还要就是如何通过 trie 树来实现敏感词的过滤,至于代码的实现,我这里就不给出了,在实现的时候,为了防止这种”麻 痹”或者“麻¥痹”等,我们也要对特殊字符进行过滤等,有兴趣的可以去实现一波。
