剑指 Offer 12. 矩阵中的路径

剑指offer最优解免费

本问题对应的 leetcode 原文链接：剑指 Offer 12. 矩阵中的路径

问题描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

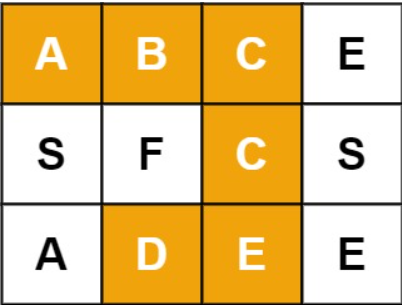
示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2:

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

限制：

m = = board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board和word仅由大小写英文字母组成

解题思路

视频讲解直达：本题视频讲解

代码实现

class Solution {
    int n;
    int m;
    int len;
    boolean[][] visited;
    public boolean exist(char[][] board, String word) {
        this.n = board.length;
        this.m = board[0].length;
        this.len = word.length();
        visited = new boolean[n][m];

        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(dsf(board, i, j, word, 0)){
                    return true;
                }
            }
        }

        return false;
    }
    boolean dsf(char[][] board, int i, int j, String word, int k){
        // 判断是否越界，已经访问过或者不匹配
        if(i < 0 || i >= n || j < 0 || j >= m || board[i][j] != word.charAt(k)){
            return false;
        }

        if(k == len - 1){
            return true;
        }
        //visited[i][j] = true;
        board[i][j] = '\n';
        // 四个方向都搜索一下
        boolean res = dsf(board, i, j + 1, word, k + 1) ||
                      dsf(board, i + 1, j, word, k + 1) ||
                      dsf(board, i, j - 1, word, k + 1) ||
                      dsf(board, i - 1, j, word, k + 1);

        board[i][j] = word.charAt(k);
        return res;
        // 时间复杂度：mn * 3^len
    }
}

时间复杂度：O(3^K * MN) ：最差情况下，需要遍历矩阵中长度为 KK 字符串的所有方案，时间复杂度为 O(3^K)；矩阵中共有 MN 个起点，时间复杂度为 O(MN)
空间复杂度：O(k)

Python

class Solution(object):
    def exist(self, board, word):
        """
        :type board: List[List[str]]
        :type word: str
        :rtype: bool
        """
        n = len(board)
        m = len(board[0])
        l = len(word)
        visited = [[False] * m for _ in range(n)]

        def dfs(i, j, k):
            if i < 0 or i >= n or j < 0 or j >= m or visited[i][j] or board[i][j] != word[k]:
                return False

            if k == l - 1:
                return True

            visited[i][j] = True
            res = dfs(i, j + 1, k + 1) or dfs(i + 1, j, k + 1) or dfs(i, j - 1, k + 1) or dfs(i - 1, j, k + 1)
            visited[i][j] = False

            return res

        for i in range(n):
            for j in range(m):
                if dfs(i, j, 0):
                    return True

        return False

C++

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        int n = board.size();
        int m = board[0].size();
        int l = word.size();
        vector<vector<bool>> visited(n, vector<bool>(m, false));

        function<bool(int, int, int)> dfs = [&](int i, int j, int k) -> bool {
            if (i < 0 || i >= n || j < 0 || j >= m || visited[i][j] || board[i][j] != word[k]) {
                return false;
            }

            if (k == l - 1) {
                return true;
            }

            visited[i][j] = true;
            bool res = dfs(i, j + 1, k + 1) || dfs(i + 1, j, k + 1) || dfs(i, j - 1, k + 1) || dfs(i - 1, j, k + 1);
            visited[i][j] = false;

            return res;
        };

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (dfs(i, j, 0)) {
                    return true;
                }
            }
        }

        return false;
    }
};

Go

func exist(board [][]byte, word string) bool {
    n := len(board)
    m := len(board[0])
    l := len(word)
    visited := make([][]bool, n)
    for i := range visited {
        visited[i] = make([]bool, m)
    }

    var dfs func(int, int, int) bool
    dfs = func(i, j, k int) bool {
        if i < 0 || i >= n || j < 0 || j >= m || visited[i][j] || board[i][j] != word[k] {
            return false
        }

        if k == l-1 {
            return true
        }

        visited[i][j] = true
        res := dfs(i, j+1, k+1) || dfs(i+1, j, k+1) || dfs(i, j-1, k+1) || dfs(i-1, j, k+1)
        visited[i][j] = false

        return res
    }

    for i := 0; i < n; i++ {
        for j := 0; j < m; j++ {
            if dfs(i, j, 0) {
                return true
            }
        }
    }

    return false
}

JS

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    // 初始化变量
    let n = board.length;
    let m = board[0].length;
    let len = word.length;
    let visited = new Array(n).fill().map(() => new Array(m).fill(false));

    // 开始搜索
    for(let i = 0; i < n; i++){
        for(let j = 0; j < m; j++){
            if(dsf(board, i, j, word, 0)){
                return true;
            }
        }
    }

    return false;
};

function dsf(board, i, j, word, k) {
    // 判断是否越界，已经访问过或者不匹配
    if(i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] !== word.charAt(k)){
        return false;
    }

    if(k === word.length - 1){
        return true;
    }

    board[i][j] = '\n';
    // 四个方向都搜索一下
    let res = dsf(board, i, j + 1, word, k + 1) ||
              dsf(board, i + 1, j, word, k + 1) ||
              dsf(board, i, j - 1, word, k + 1) ||
              dsf(board, i - 1, j, word, k + 1);

    board[i][j] = word.charAt(k);
    return res;
    // 时间复杂度：mn * 3^len
}

剑指offer题解